Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
"((()))", "(()())", "(())()", "()(())", "()()()"
这道题也是深度优先算法题目。
方案一:错误的解法
在一开始附设一个标记数组,后来自以为没有什么用处,就去掉了,然后得出了下面的代码,以及下面的结果。
#include <stdio.h>
#include <stdlib.h>
void DFS(char *buf,int begin,int end,int n)
{
if(begin >= end){
if(end == n)
puts(buf);
return ;
}
buf[begin] = '(';
for(int w = begin+1;w <= end;w += 2){
buf[w] = ')';
DFS(buf,begin+1,w-1,n);
DFS(buf,w+1,end,n);
}
}
void DFSTraverse(int n)
{
if(n <= 0)
return;
char *buf = (char *)malloc((2*n + 1)*sizeof(char));
buf[2*n] = '\0';
DFS(buf,0,2*n-1,2*n-1);
}
int main()
{
int n;
while(scanf("%d",&n) != EOF){
DFSTraverse(n);
}
return 0;
}
最后两行输出的结果少。关键原因在于
for(int w = begin+1;w <= end;w += 2){
buf[w] = ')';
DFS(buf,begin+1,w-1,n);
DFS(buf,w+1,end,n);
}当第一个DFS求出buf[1…4]的()()结果后,并没有输出,然后求出(())结果,并退出,进行该循环中的下一个DFS()。
解决的方法,还是附设一个标记数组来求解。
方案二:
想到了附设数组,但是还是没有很好的解决问题,翻看了以前写的代码,当时还不会什么算法结构,只是自己想出来的……
算法中也是附设了标记数组,并且在函数参数中附设了剩余要求的个数。
并且在其中判断了a[j+1] == 1,如果成立,就表明已经到了内层循环的边界,就退出循环!当时想到了,现在竟然没有想到……
/*主要思想是,确定第一个和第几个匹配,在此基础上,再细致划分
*第一类:第一个和第二个匹配,然后剩余四个位置,有两种情况
*第二类:第一个和第四个匹配,那么第二个和第三个匹配,第五个和第六个匹配,只有这一种情况
*第三类:第一个和第六个匹配,中间四个位置,有两种情况
*对于第二类,必须判断 if(a[j+1]==1) break; 这样才可以!
*/
#include <stdio.h>
#include <stdlib.h>
#define MAX 20
#define N 8
void BracketPair(int n,int a[],char buf[])
{
//如果还有位置则继续填充,否则,输出数组的内容
int i,j;
if(n>0){ //找到第一个需要填空的地方
for(i=0;i<N;i++){
if(a[i]==0){
a[i]=1;
buf[i] = '(';
break;
}
}
//找到后,进行赋值
for(j=i+1;j<N;j+=2){
/* 这里不用像66题那样去判断,因为是匹配的,一定能满足在a[j]==0!
while(j<N && a[j])
j+=2;
if(j>=N)
break;
*/
a[j]=1;
buf[j]=')';
BracketPair(n-2,a,buf);
a[j]=0;
if(a[j+1]==1) //这里是为了防止第二类的时候,多算情况
break;
}
a[i]=0;
}
else{
for(i=0;i<N;i++)
printf("%c",buf[i]);
printf("\n");
}
}
int main(void)
{
char buf[MAX];
int a[MAX]={0};
while(1){
printf("input a to continue:");
while(getchar() != 'a')
;
BracketPair(N,a,buf);
}
return 0;
}
方案三:
利用DFS算法再次来求解:
void DFS(int *visited,char *buf,int n)
{
int i;
for(i = 0;i < n;i++){
if(visited[i] == 0)
break;
}
if(i == n){
puts(buf);
return;
}
visited[i] = 1;
buf[i] = '(';
for(int j = i+1;j < n;j+=2){
visited[j] = 1;
buf[j] = ')';
DFS(visited,buf,n);
visited[j] = 0; //清除标志
if(visited[j+1] == 1) //已经到达边界
break;
}
visited[i] = 0;<span style="white-space:pre"> </span>//清楚标志
}
void DFSTraverse(int n)
{
if(n <= 0)
return;
int *visited = (int *)malloc(2*n*sizeof(int));
char *buf = (char *)malloc((2*n + 1)*sizeof(char));
buf[2*n] = '\0';
memset(visited,0,2*n*sizeof(int));
DFS(visited,buf,2*n);
}
方案四:
http://blog.csdn.net/yutianzuijin/article/details/13161721
这个链接中提供了好的方法:
解答:
该问题解的个数就是卡特兰数,但是现在不是求个数,而是要将所有合法的括号排列打印出来。
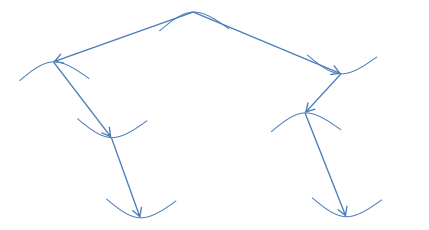
该问题和《编程之美》的买票找零问题一样,通过买票找零问题我们可以知道,针对一个长度为2n的合法排列,第1到2n个位置都满足如下规则:左括号的个数大于等于右括号的个数。所以,我们就可以按照这个规则去打印括号:假设在位置k我们还剩余left个左括号和right个右括号,如果left>0,则我们可以直接打印左括号,而不违背规则。能否打印右括号,我们还必须验证left和right的值是否满足规则,如果left>=right,则我们不能打印右括号,因为打印会违背合法排列的规则,否则可以打印右括号。如果left和right均为零,则说明我们已经完成一个合法排列,可以将其打印出来。通过深搜,我们可以很快地解决问题,针对n=2,问题的解空间如下:
于是就有以下C++代码:
void generate(int leftNum,int rightNum,string s,vector<string> &result)
{
if(leftNum==0&&rightNum==0)
{
result.push_back(s);
}
if(leftNum>0)
{
generate(leftNum-1,rightNum,s+'(',result);
}
if(rightNum>0&&leftNum<rightNum)
{
generate(leftNum,rightNum-1,s+')',result);
}
}用C++实现确实很简单,可以再字符串后面直接加上某个字符即可。但用C的话,就麻烦了,个人实现代码如下
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void DFS(char *buf,int leftnum,int rightnum,int index)
{
if(leftnum == 0 && rightnum == 0){
puts(buf);
return ;
}
if(leftnum > 0){
buf[index] = '(';
DFS(buf,leftnum-1,rightnum,index+1);
}
if(rightnum > 0 && rightnum>leftnum){
buf[index] = ')';
DFS(buf,leftnum,rightnum-1,index+1);
}
}
void DFSTraverse(int n)
{
if(n <= 0)
return;
char *buf = (char *)malloc((2*n + 1)*sizeof(char));
buf[2*n] = '\0';
DFS(buf,n,n,0);
}
int main()
{
int n;
while(scanf("%d",&n) != EOF){
DFSTraverse(n);
}
return 0;
}
确实,算法比较好了,能得到很好的结果,也容易写出简单高效的代码。
说明:
这个解法的关键在于,设置了一个index索引,在深层次的地方和浅层次的地方index不一样,通过这个避免了下面递归解法中的出栈入栈等问题。与这种方法的相似的题目是:
Letter Combinations of a Phone Number
上述链接中还提供了一个递归算法,如下:
作为一个例子,看一下数组的入栈出栈顺序问题:给定一个长度为n的不重复数组,求所有可能的入栈出栈顺序。该问题解的个数也是卡特兰数,根据上面的思路,我们也可以写出一个类似的代码:
void inoutstack(int in,int out,deque<int> &q,stack<int> &s,deque<int> seq,vector<deque<int>> &result)
{
if(!in&&!out)
{
result.push_back(q);
return;
}
if(in>0)
{
s.push(seq.front());
seq.pop_front();
inoutstack(in-1,out,q,s,seq,result);
seq.push_front(s.top());
s.pop();
}
if(out>0&&in<out)
{
q.push_back(s.top());
s.pop();
inoutstack(in,out-1,q,s,seq,result);
s.push(q.back());
q.pop_back();
}
}上述代码由于采用了栈和队列模仿整个过程,所以显得略微复杂,但是代码的基本结构还是符合一个类似的基本规则:在某一个特定时刻,入栈的次数大于或者等于出栈的次数。在生成括号的问题中,我们利用一个string来保存结果,由于打印左括号时不影响打印右括号,所以无需复杂的状态恢复。在入栈出栈顺序问题中,由于两次递归调用共享同一个栈和队列,所以我们需要手动恢复其内容。在恢复时,队列会从头部删除和添加,所以我们采用了deque,它可以在头部添加和删除元素。queue只能在头部删除元素,所以没有采用。