LeetCode | Rotate Image（旋转图像）

2023年4月11日 320次阅读

You are given an n x n 2D matrix representing an image.

Rotate the image by 90 degrees (clockwise).

Follow up:
Could you do this in-place?

题目解析：

题目不难，只是旋转，但要仔细换图看清楚旋转的坐标。

方案一：

[i,j]–>[j,n-1-i]–>[n-1-i,n-1-j]–>[n-1-j,i]

还是有一定规律的，坐标向右走的时候，y1=x0，x1=n-1-y0。

如果正向的话要一点一点保存要赋给的位置，那么坐标找到了，逆时针赋值，会更简单。

坐标范围中，j<n-i-1,必须小于，因为n-i-1已经被转移了。

class Solution {
public:
    void rotate(vector<vector<int> > &matrix) {
        int n = matrix.size();
        if(n<=1)
            return ;
        for(int i = 0;i < n/2;i++){
            for(int j = i;j < n-i-1;j++){
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[n-1-j][i];
                matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
                matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
                matrix[j][n-1-i] = tmp;
            }
        }
    }
};

方案二：

《LeetCode | Rotate Image（旋转图像）》


class Solution {
public:
    void rotate(vector<vector<int> > &matrix) {
        int i,j,temp;
        int n=matrix.size();
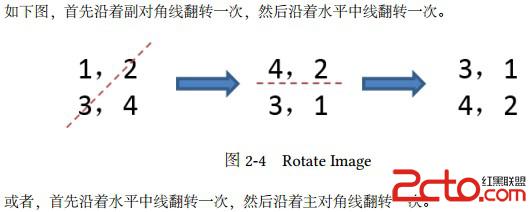
        // 沿着副对角线反转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n - i; ++j) {
                temp = matrix[i][j];
                matrix[i][j] = matrix[n - 1 - j][n - 1 - i];
                matrix[n - 1 - j][n - 1 - i] = temp;
            }
        }
        // 沿着水平中线反转
        for (int i = 0; i < n / 2; ++i){
            for (int j = 0; j < n; ++j) {
                temp = matrix[i][j];
                matrix[i][j] = matrix[n - 1 - i][j];
                matrix[n - 1 - i][j] = temp;
            }
        }
    }
};


点赞