问题

用递归方式遍历二叉树

思路说明

遍历二叉树的方法有广度优先和深度优先两类，下面阐述的是深度优先。

以下图的二叉树为例：

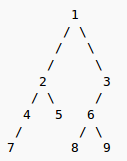
先定义三个符号标记：

• 访问结点本身（N）
• 遍历该结点的左子树（L）
• 遍历该结点的右子树（R）

有四种方式：

1. 前序遍历(PreorderTraversal,NLR):先访问根结点，然后遍历其左右子树
2. 中序遍历(InorderTraversal,LNR):先访问左子树，然后访问根节点，再访问右子树
3. 后序遍历(PostorderTraversal,LRN):先访问左右子树，再访问根结点
4. 层序遍历(levelorderTraversal):按照从上到下的层顺序访问

上面的数，按照以上四种方式遍历，得到的结果依次是：

1. preorder: 1 2 4 7 5 3 6 8 9
2. inorder: 7 4 2 5 1 8 6 9 3
3. postorder: 7 4 5 2 8 9 6 3 1
4. level-order: 1 2 3 4 5 6 7 8 9

下面用递归的方式，解决此题。

解决(Python)

#! /usr/bin/env python
#coding:utf-8

from collections import namedtuple
from sys import stdout

Node = namedtuple('Node', 'data, left, right')
tree = Node(1,
            Node(2,
                 Node(4,
                      Node(7, None, None),
                      None),
                 Node(5, None, None)),
            Node(3,
                 Node(6,
                      Node(8, None, None),
                      Node(9, None, None)),
                 None))


#前序（pre-order，NLR）

def preorder(node):
    if node is not None:
        print node.data,
        preorder(node.left)
        preorder(node.right)


#中序（in-order，LNR）

def inorder(node):
    if node is not None:
        inorder(node.left)
        print node.data,
        inorder(node.right)


#后序（post-order，LRN）

def postorder(node):
    if node is not None:
        postorder(node.left)
        postorder(node.right)
        print node.data,


#层序（level-order）

def levelorder(node, more=None):
    if node is not None:
        if more is None:
            more = []
        more += [node.left, node.right]
        print node.data,
    if more:    
        levelorder(more[0], more[1:])

if __name__=="__main__"
    print '  preorder: ',
    preorder(tree)
    print '\t\n   inorder: ',
    inorder(tree)
    print '\t\n postorder: ',
    postorder(tree)
    print '\t\nlevelorder: ',
    levelorder(tree)
    print '\n'